Kruskal 알고리즘이란
- greedy method를 이용하여 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최족 해답을 구하는 것
- greedy method
- 결정을 해야 할 때마다 그 순간에 가장 좋다 생각되는 것을 선택함으로써, 최종적인 해답에 도달
- 그 순간에는 최적이지만, 전체적인 관점에서 최적이라는 보장이 없기 때문에 반드시 검증해야 한다
- Kruskal 알고리즘은 최적의 해답을 주는 것으로 증명되어 있다
- MST(Minimum Spanning Tree, 최소 비용 신장 트리)가
1)최소 비용의 간선으로 구성됨
2) 사이클을 포함하지 않음
의 조건에 근거하여 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택한다
- spanning tree는 모든 간선을 지나는 tree이다
Kruskal 알고리즘의 동작
1. 그래프의 간선들을 가중치의 오름차순으로 정렬한다
2. 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다
- 즉, 가장 낮은 가중치를 먼저 선택한다
- 사이클을 형성하는 간선을 제외한다
3. 해당 간선을 현재의 MST의 집합에 추가한다
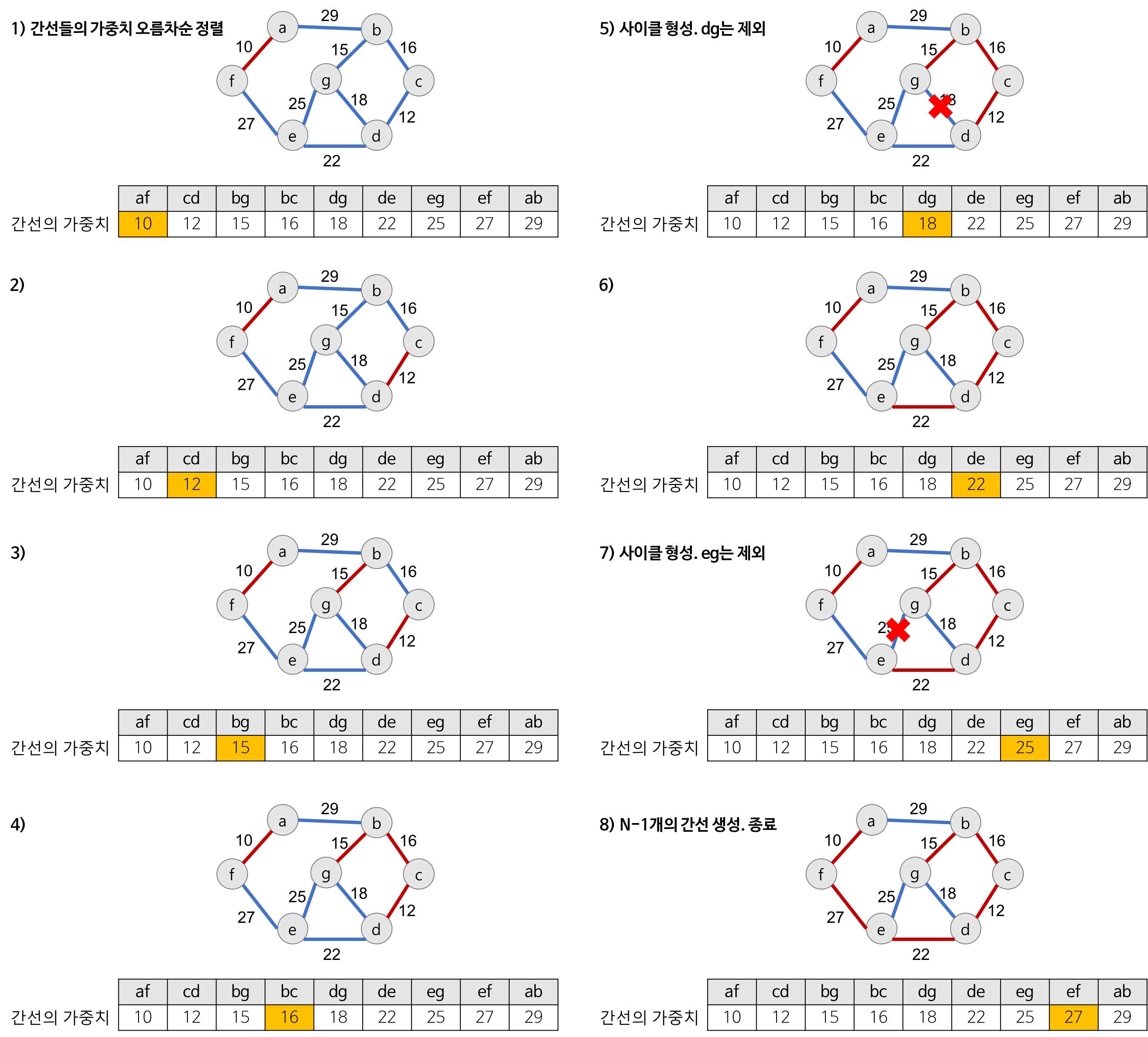
Kruskal 알고리즘의 구체적인 동작 과정
- 간선 선택을 기반으로 하는 알고리즘
- 이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법
주의할 점
- 다음 간선을 이미 선택한 간선들의 집합에 추가할 때 사이클을 생성하는지 체크하기
- 새로운 간선이 이미 다른 경로에 의해 연결되어 있는 정점들들 연결할 때 사이클이 형성된다
- 즉, 추가할 새로운 간선의 양끝 정점이 같은 집합에 속해있으면 사이클이 생성된다
- 사이클 생성 여부를 확인하는 방법
- union-find 알고리즘 이용
시간 복잡도
- union-find 알고리즘을 이용하면 Kruskal 알고리즘의 시간 복잡도는 간선들을 정렬하는 시간에 좌우된다
- 즉, 간선 e개를 효율적인 알고리즘으로 정렬하면
- Kruskal 알고리즘의 시간 복잡도는 O(elog2e)가 된다
Prim 알고리즘이란
- 시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장해나가는 방법
Prime 알고리즘의 동작
1. 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다
2. 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다
- 즉, 가장 낮은 가중치를 먼저 선택한다
3. 위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다
Prim 알고리즘의 구체적인 동작 과정
- 정점 선택을 기반으로 하는 알고리즘
- 이전 단계에서 만들어진 신장 트리를 확장하는 방법

Prim 알고리즘의 시간 복잡도
- 주 반복문이 정점의 수 n만큼 반복하고, 내부 반복문이 n번 반복
- Prim 알고리즘의 시간 복잡도는 O(n2)이 된다
- Kruskal 알고리즘의 시간 복잡도는 O(elog2e) 이므로
- 그래프 내 간선 숫자가 적은 sparse graph에서는 Kruskal이 적합하고
- 그래프 내 간선 숫자가 많은 dense graph에서는 Prim 알고리즘이 적절하다
'Coding > 알고리즘' 카테고리의 다른 글
| Greedy 알고리즘이란 (0) | 2020.10.04 |
|---|---|
| Binary Search란 (0) | 2020.10.03 |
| Dynamic Programming이란 (0) | 2020.10.01 |
| 그래프 - 인접 행렬과 인접 리스트 (0) | 2020.09.30 |


