1. Loss function, Cost function, Objective function의 차이
사실 위의 세 가지 function은 거의 같은 맥락으로 쓰인다고 보면 된다. 하지만 굳이 차이를 나눠보자면 다음과 같다고 한다.
모델을 학습할 때는 비용(cost), 즉 오류를 최소화하는 방향으로 진행된다
비용이 최소화되는 곳이 성능이 가장 잘 나오는 부분이며, 가능한 비용이 적은 부분을 찾는 것이 최적화(Optimization)이고 일반화(Generalization)의 방법이다
이 비용(cost) 혹은 손실(loss)이 얼마나 있는지 나타내는 것이 비용함수(cost function), 손실함수(loss function)이라고 할 수 있다
비용/손실을 표시하는 함수로는 다음 세가지 loss function, cost function, objective function이 있다
- Loss fucntion

- Cost function

Loss function의 합, 평균 에러를 확인한다
- Objective function

모델에 대해 가장 일반적으로 사용하는 용어로써 최댓값, 최솟값을 구하는 함수를 말한다
2. Softmax Regression
* Sigmoid, Logit, Softmax 사이 관계
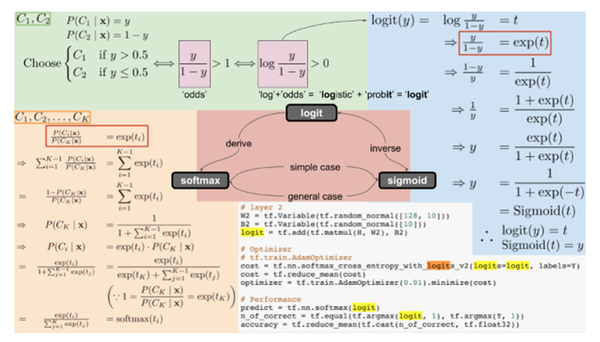
- Logit과 Sigmoid는 서로 역함수 관계
- 2개 클래스 대상으로 정의하던 logit을 K개의 클래스 대상으로 일반화하면 softmax 함수 유도
- Softmax 함수에서 K를 2로 놓으면 sigmoid 함수로 환원
- 반대로 sigmoid 함수를 K개의 클래스 대상으로 일반화하면 softmax 함수 유도
- Sigmoid function: 인공신경망에서 ReLU가 등장하기 이전 활발하게 사용되었던 activation function이다, hidden layer 바로 뒤에 부착된다
-> sigmoid: 마지막 단에서 많이 쓰이고, ReLU: 내부에서 많이 쓰인다. sigmoid도 현재 활발히 쓰이긴 한다
- Softmax function: 인공신경망이 내놓은 K개의 클래스 구분 결과를 확률처럼 해석하도록 만들어준다. 보통 output 노드 바로 뒤에 부착한다
차이점: 수학적으로는 같은 함수이고, 다루는 클래스가 2개(sigmoid)이냐 K개(softmax)이냐
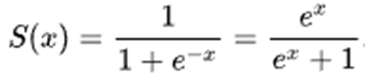
sigmoid
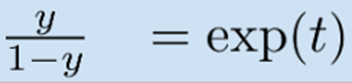
logit
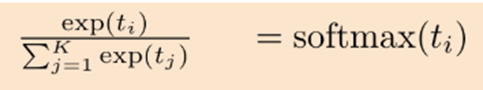
softmax
출처:https://opentutorials.org/module/3653/22995
logit, sigmoid, softmax의 관계 - 한 페이지 머신러닝
[logit, sigmoid, softmax의 관계] 이번에는 logit, sigmoid, softmax의 관계에 대해서 알아보겠습니다. 이것들이 서로 다 다른 개념같지만 서로 매우 밀접하게 관련이 있는데요. 그림의 가운데 부분에서 세 개념의 관계를 화살표로 엮어놓았습니다. 결론부터 일단 말씀드리면 - logit과 sigmoid는 서로 역함수 관계이고 - 2개 클래스를 대상으로 정의하던 logit을 K개의 클래스를 대상으로 일반화하면 softmax함수
opentutorials.org
* Softmax
- Neural network의 최상위층에 사용하여 classification을 위한 function으로 사용된다
- NN의 최상위 계층에 sigmoid function을 사용하여 실제값과 출력값의 차이를 error function으로 사용해도 되지만, softmax를 사용하는 주된 이유는 결과를 확률값으로 해석하기 위함이다
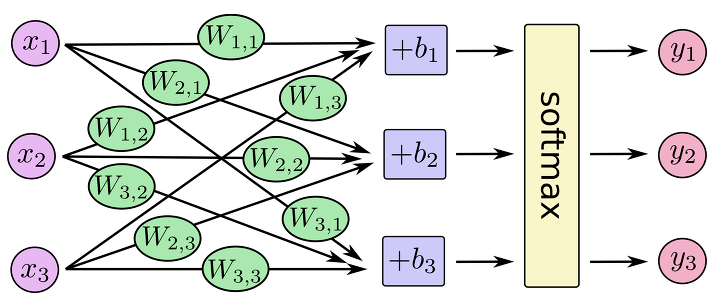
위의 그림에서, y1 + y2 + y3 = 1이다!
- 모든 합이 1이미르 어떠한 label의 확률이 높아지면 다른 label이 가지는 확률값은 그에 따라서 내려간다 -> softmax의 사용은 normalization의 효과를 얻는다
출처: https://mongxmongx2.tistory.com/30
Softmax
Softmax Softmax function은 Neural network의 최상위층에 사용하여 Classification을 위한 function으로 사용한다. NN의 최상위 계층에 사실 Sigmoid function을 사용하여 실제값과 출력값을 차이를 error functi..
mongxmongx2.tistory.com
3. Negative log likelihood
* Likelihood(가능도/우도)란
- 주어진 데이터가 가정한 모델에 얼마나 적합한지에 대한 조건부 확률 - likelihood가 높아질수록 모델이 관측된 데이터를 잘 표현한 것
* Negative log likelihood
- 입력값 X와 parameter θ가 주어졌을 때 정답 Y가 나타낼 확률, 즉 likelihood P(Y|X;θ)를 최대화하는 θ가 우리가 찾고 싶은 결과이다
- 학습데이터의 각각의 likelihood를 log scale로 바꾸어도 argmax의 결과는 바뀌지 않으므로, likelihood의 곱을 최대로 만드는 θ와 log likelihood의 기대값을 최대로 하는 θ는 같다
* log scale + negative scale 처리를 하는 이유
- Log scale로 likelihood를 바꾸면 학습이 잘 될수록 loss가 증가하는 상태가 된다
- 학습이 잘 될수록 target과 output 사이 gap이 줄어들어 loss가 감소하는 것을 표현해야 한다
-> negative scale을 적용시켜 준다
- x가 1일때 cost를 0으로, x가 0일때 cost는 큰 양수값으로 된다
* 장점
- 우리가 만드려는 모델에 다양한 확률분포를 가정할 수 있게 되어 유연하게 대응 가능하다
- NLL로 딥러닝 모델의 손신을 정의하면 이는 곧 두 확률분포 사이의 차이를 재는 함수인 크로스 엔트로피가 된다
- 크로스 엔트로피는 비교 대상 확률분포의 종류를 특정하지 않는다
- 최종 output node의 가능한 node(예시) - Linear unit, Sigmoid unit, Softmax unit
-> output node의 output과 우리가 가진 target(데이터 분포) 차이가 곧 cross entropy
-> 이 차이(cross entropy)만큼을 loss로 보고 이 loss에 대한 gradient를 구해서 역전파 하는 과정: 딥러닝의 학습
-> 즉, 각 확률분포에 맞는 loss를 따로 정의할 필요 없이 NLL만 써도 되고(loss function으로써), output node의 종류만 바꾸면 세 개의 확률분포에 대응할 수 있다

출처: http://blog.naver.com/PostView.nhn?blogId=qbxlvnf11&logNo=221386519587
머신러닝 - 손실 함수(Loss Function)의 종류
(본 글은 책 '처음 배우는 머신러닝'의 일부를 참고하였습니다.)우리는 최적화(Optimization) 과정을 통해...
blog.naver.com
https://ratsgo.github.io/deep%20learning/2017/09/24/loss/
딥러닝 모델의 손실함수 · ratsgo's blog
이번 글에서는 딥러닝 모델의 손실함수에 대해 살펴보도록 하겠습니다. 이 글은 Ian Goodfellow 등이 집필한 Deep Learning Book과 위키피디아, 그리고 하용호 님의 자료를 참고해 제 나름대로 정리했음을 먼저 밝힙니다. 그럼 시작하겠습니다. 딥러닝 모델의 손실함수로 음의 로그우도(negative log-likelihood)가 쓰입니다. 어떤 이유에서일까요? 딥러닝 모델을 학습시키기 위해 최대우도추정(Maximum Likelihood Es
ratsgo.github.io
https://ljvmiranda921.github.io/notebook/2017/08/13/softmax-and-the-negative-log-likelihood/
Understanding softmax and the negative log-likelihood
In this notebook I will explain the softmax function, its relationship with the negative log-likelihood, and its derivative when doing the backpropagation al...
ljvmiranda921.github.io
4. Cross Entropy
식:

* Cross Entropy란
- 두 확률분포 p와 q 사이의 차이를 계산하는 데 cross entropy 함수가 사용된다, 즉 오차계산이다
- 여기에서 p = P(Y|X) -> 우리가 가진 데이터의 분포, q = P(Y|X;θ) -> 모델이 예측한 결과의 분포
- 위의 상황에서 Cross Entropy는 parameter θ 하에서 negative log likelihood의 기대값이라고 해석할 수 있다
- 즉,
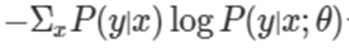
를 최소화하는 θ가 바로 우리가 찾고싶은 모델이다
- 2개의 확률 분포의 차이를 나타내는 용도로 정의
* Cross entropy와 log likelihood와의 관계
- Log Likelihood 곱이 최대인 모델 찾기
- Log likelihood 기대값이 최대인 모델 찾기
- 학습데이터의 분포(distribution)와 모델이 예측한 결과 분포 사이 차이 최소화
- Cross Entropy 최소화하기
---> 모두 같은말!
* Entropy란?
- 정보의 Entropy란
-> 정보(information): degree of surprise, 놀람의 정도
-> 정보량: h(x) = -logP(x), P(x)는 확률이고 사건 x의 정보량 h(x)
-> 자주 발생하는 관찰이나 사건은 작은 값, 자주 발생하지 않는 관찰이나 사건은 큰 값
- Entropy
-> 정보량(놀람의 정도)들의 평균
-> 확률변수의 평균 정보량 = 놀람의 평균적인 정도 = 불확실성의 정도(확률분포의 무작위성)
-> entropy H[x] E[-logP(x)] =
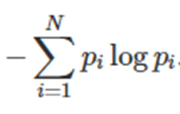
* Entropy 예시
- X = 0, 1인 확률 공간에서 확률값이 다른 3가지 예시
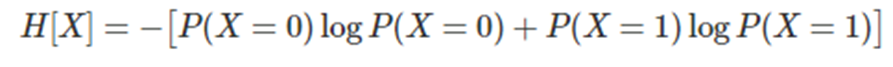
1) 엔트로피 최대일때

2)
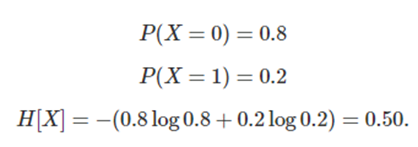
3) 불확실성이 없는 상태
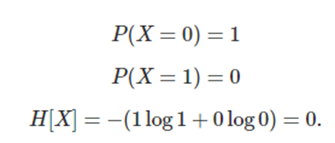
- 이산확률변수 X가 균일분포(uniform distrubiton)일 때 평균 정보량 H[X], 즉 엔트로피가 최대값이다
* KL Divergence(Relative entropy) - Kullback-Leibler divergence
- 두 확률분포 p와 q가 얼마나 다른지를 측정
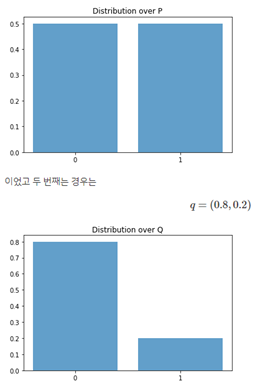

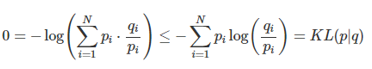
* Cross Entropy 사용할 때 주의사항
- label의 값이 one-hot encoding일때만 사용 가능하다
- one-hot encoding: mutlinomial classification에서 사용하는 인코딩 방법으로 출력값의 형태가 정답 label은 1이고 나머지 label 값은 모두 0
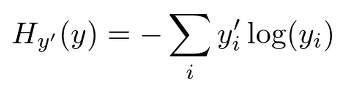

* MSE와 Cross Entropy 비교 - MSE보다 Cross Entropy를 사용하는 이유
- Cross Entropy cost function이 Neural Networks의 학습속도 저하(slowdown)을 막는다
- Cost Function의 일반적인 형태: Mean Square Error(MSE) Cost Function

* MSE의 문제점
- Sigmoid function을 activation function으로 쓸 경우, t값이 너무 크거나 작아지면 미분값이 급격히 0에 가까워지는 현상이 발생한다. 이는 학습속도 저하 문제를 유발한다
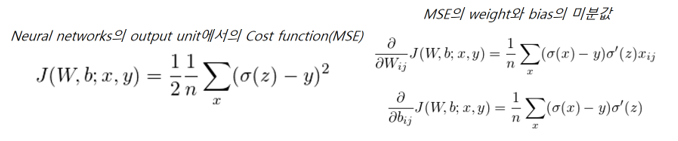
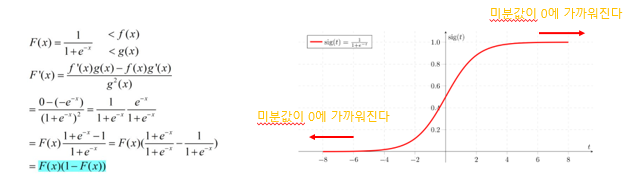
- 이런 문제로 인해 NN(Neurla Networks)를 학습시키기 위해 Cost Function 대신 Cross Entropy Cost Function을 사용한다

-> 오차가 더 큰 input에 대해서는 더 많이 업데이트
-> 오차가 더 작은 input에 대해서는 더 적게 업데이트
출처: https://ratsgo.github.io/deep%20learning/2017/09/24/loss/
https://icim.nims.re.kr/post/easyMath/550
Entropy, Cross-entropy, KL Divergence | 알기 쉬운 산업수학 | 산업수학혁신센터
icim.nims.re.kr
https://worthpreading.tistory.com/23
Cross entropy error, CEE (교차 엔트로피 오차)
cross entropy error 함수는 softmax를 활성화함수로 사용할 때 주로 사용되는 cost function(손실함수)이다. 우선 수식부터 살펴보자 여기서 H(y)는 cost를 나타낸다. 자, 이제 왜 이런 모양을 가지는지 한번 알..
worthpreading.tistory.com
http://solarisailab.com/archives/2237
Neural Networks의 학습속도 저하(slowdown)를 막는 Cross-Entropy Cost function | 솔라리스의 인공지능 연구실
solarisailab.com
5. Binary Cross Entropy
* Binary Cross Entropy란
- Probabilistic classification model 학습: probabilistic prediction이 ground-truth probabilities와 최대한 유사하게끔 모델 파라미터를 조절
- 즉, output과 target의 probability가 유사하게 모델 파라미터를 조절
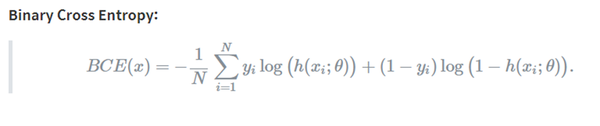
- BCE(Binary Cross Entropy)는 두 개의 class 중 하나를 예측하는 task에 대한 cross entropy의 special case이다
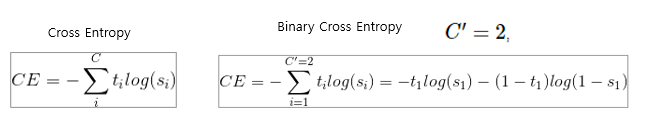
* Multi-label classification이란
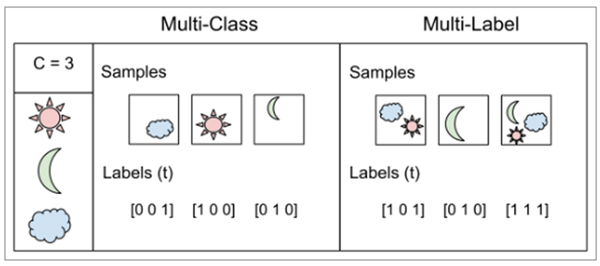
- Mutli-class classification
class가 여러개이고, label은 각 class 하나만을 나타낸다. 위의 예시처럼 한 집단에 클래스가 [구름, 해, 달] 3가지가 있고 각 label은 각각 구름, 해, 달 중 한가지만 가질 수 있다. one-hot encoding으로 나타내질 수 있다
- Multi-label classification
multi-label classifiation처럼 class가 여러개이고 label에도 여러 class가 해당될 수 있다. 위의 예시처럼 class는 [구름, 해, 달]이고 각 label은 동시에 구름과 달을 포함할 수 있다
* Multi-label classifiation이라고 생각 가능한 경우
위의 예시처럼 하나의 집단 안에서의 여러 class에 대해, label이 여러 class가 가능한 경우를 multi-label classification이라고 보았다
하지만 여러 class를 가진 집단 자체가 여러개이고, 각 집단에서의 single class classification을 분류하는 문제 또한 multi-label classification으로 볼 수 있을 것이다
설명으로 하면 복잡하니 그림으로 확인하자

Multi-label classification - 1
첫 번째는 위의 예시처럼 한 집단에 3개의 class가 있고, label은 여러 class를 나타낼 수 있다. 이는 전형적인 multi-label classification이다.
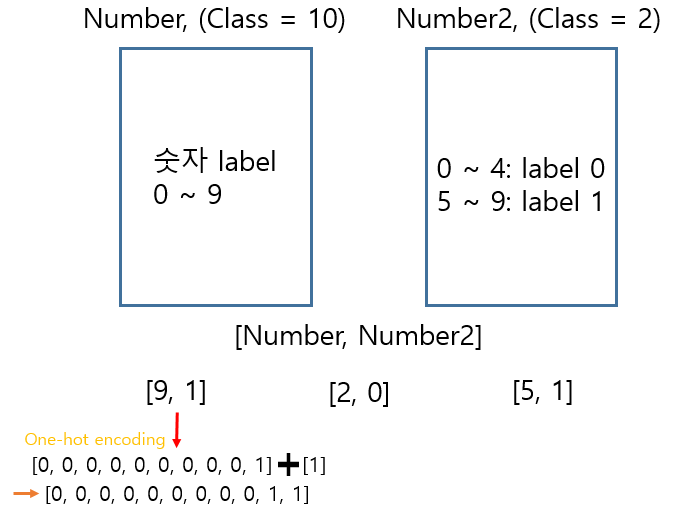
Multi-label classification - 2
두 번째는 여러 class를 가지는 집단이 여러개일 때, 각 집단에서는 single class classification이지만 각 집단별로 어떤 class인지를 한 번에 알아내는 것 또한 결과적으로 multi-label classification이 될 수 있다.
즉 output이 각각 [9, 1], [2, 0], [5, 1]이라면, 즉 one-hot encoding을 통해 나타내면
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1], [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1] 과 같이 나타낼 수 있다. 이같은 경우에도 BCE를 사용하면 multi-label classification이 가능하다.
하지만 각 집단 별로 각각 label을 찾는 경우, 즉 output을 [0, 0, 0, 0, 0, 0, 0, 0, 0, 1] 과 [1] 이렇게 두 개로 찾을 때에는 BCE를 사용하면 안되고 softmax 등을 이용하여 single label classification을 각각 수행해주어야 한다. model을 만들때 single label classification을 각각의 집단에서 수행해주고 출력을 한번에 하는 등의 방법을 이용하면 될 것이다.
* Multi-label classification에 BCE를 사용하는 이유
- multi-label classification의 경우에, output layer에 sigmoid, cost function으로 BCE를 사용하면 좋다
- sigmoid는 softmax와 다르게 output에 대해 probability distribution을 제공하지 않고 independent probabilities를 제공한다
-> 앞에서 말한 것처럼 softmax는 전체 합이 1이 되는 확률분포로 나타내므로 각 distribution간에 영향을 받는다. 한 node의 확률분포가 높아지면 다른 분포는 낮아지는 식으로 서로의 확률분포에 영향을 끼친다
-> 하지만 sigmoid는 probabilities가 다른 node에 영향을 받지 않고 독립적으로 값을 가진다
- 즉, every output vector component에 대해 loss를 계산하여 other component values에 영향을 받지 않는다 -> multi-label classification에 사용하는 이유
출처: https://curt-park.github.io/2018-09-19/loss-cross-entropy/
[손실함수] Binary Cross Entropy
확률, 정보이론 관점에서 살펴보는 Binary Cross Entropy 함수
curt-park.github.io
https://gombru.github.io/2018/05/23/cross_entropy_loss
Understanding Categorical Cross-Entropy Loss, Binary Cross-Entropy Loss, Softmax Loss, Logistic Loss, Focal Loss and all those c
People like to use cool names which are often confusing. When I started playing with CNN beyond single label classification, I got confused with the different names and formulations people write in their papers, and even with the loss layer names of the de
gombru.github.io
What loss function for multi-class, multi-label classification tasks in neural networks?
I'm training a neural network to classify a set of objects into n-classes. Each object can belong to multiple classes at the same time (multi-class, multi-label). I read that for multi-class probl...
stats.stackexchange.com
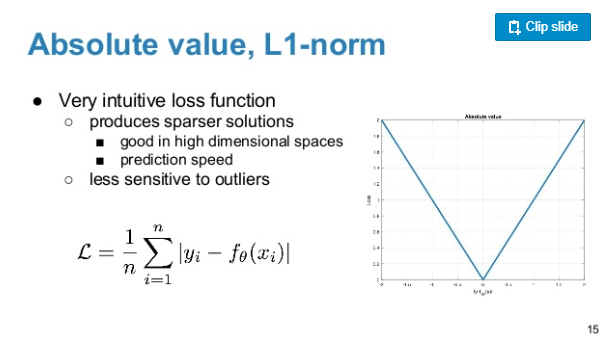
6. Euclidean loss, L1 norm, L2 norm
L1-nrom: Absolute value
L2-norm: Square error, Euclidean loss


직관적으로 L1, L2, Ln 이해하기
'Machine Learning & Deep Learning' 카테고리의 다른 글
| Active Learning이란 (0) | 2020.09.16 |
|---|---|
| AI(Artificial Intelligence), ML(Machine Learning), DL(Deep Learning) 차이점 알아보기 (0) | 2020.01.23 |
| 딥러닝 프레임워크 - Tensorflow vs PyTorch (0) | 2019.12.18 |


